円周率.jp - 基底

FFT の計算時間オーダーが $O(n \log n)$ になることについては DFT をサイズが半分の DFT 2つに分割する形で説明した。この様に DFT を 2 つに分けていく FFT を 2 基底 FFT という。しかし FFT を行う上で基底、すなわち分割数は 2 以外でも自由に取ることができる。

また、基底の異なる FFT をコンピュータプログラムとして動作させる場合、演算量や演算量に対するメモリ読み書きの割り合いなどが原因となり速度に違いが出てくる。

ここでは 2 基底、3 基底、 4 基底の FFT を具体例とし、FFT の概念的な説明とそれらをプログラムで実装する際の演算の省略について説明する。

2 基底 FFT

まずは基本となる 2 基底 FFT の説明を行う。簡単のため $n=2^e$ としよう。

本来 DFT を行うデータは 1 次元であるが、Self-sorting 型 FFT のアルゴリズムを考える場合は 2 次元に再配置すると分かりやすい。より詳細に言うなら「長さ $W$ の配列を $H$ 個組み合わせた 2 次元データ」が 2 つ、と考える。(各変数の値は下記擬似コード参照)

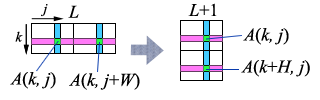
計算の過程としては図 1 のように高さ $H$、幅 $W$ の四角形を 2 個並べることになる。各ステップでは横並びにした四角形それぞれ 1 つずつ値を取り出し、計算後は縦並びにした四角形それぞれに 1 つずつ値を書き込むことになる。具体的に時間間引き FFT のアルゴリズムは以下のようになるので実装との対応を確認してもらいたい。なお 1 次元配列との対応は $A_L[k,j]=a_{2Wk+j}$ となる。

for $L$ = 0,1,2,...,$e-1$ ：
1. $H=2^L$, $W=2^{e-L-1}$
2. for $k$ = 0,1,2,...,$H-1$ ：
  1. for $j$ = 0,1,2,...,$W-1$ ：
    1. ${\displaystyle\begin{alignat}{3} & A_{L+1}[k,&& j] = A_L[k,j] + \omega^{kW}A_L[k,j+W]\\ & A_{L+1}[k+H,&& j] = A_L[k,j] - \omega^{kW}A_L[k,j+W] \end{alignat}}$

次に演算量を再確認してみよう。 2 基底 FFT では最内ループで 1 回の複素数乗算と 2 回の複素数加減算 (以下、単純に加算で代表する) を行っている。さらにそれが $WH=n/2$ 回繰り返され、$e=\log_2n$ 回繰り返されるので、全体で $\dfrac12n\log_2 n$ 回の複素数乗算と $n\log_2n$ 回の複素数加算が、つまり $2n\log_2n$ 回の実数乗算と $3n\log_2n$ 回の実数加算が行われる。

3 基底 FFT

冒頭に書いたとおり、$O(n\log n)$ で FFT を行うためにはデータ数 $n$ が 2 のべき乗である必要はない。 2 基底 FFT と基本的な考え方を同じくすれば 3 基底 FFT を作成することが可能である。

3 基底 FFT では図 2 のように高さ $H$、幅 $W$ の四角形を 3 個並べて考える。なお 1 次元配列との対応は $A_L[k,j]=a_{3Wk+j}$ となる。

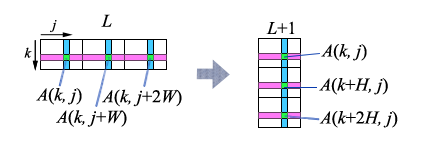
ここでは $n=3^e$ として 3 基底の FFT アルゴリズムを示す。また、表現の単純化のため $\Omega = \exp(-2\pi i/3) = \dfrac{-1-\sqrt{3}i}{2}$ とする。

for $L$ = 0,1,2,...,$e-1$ ：
1. $H=3^L$, $W=3^{e-L-1}$
2. for $k$ = 0,1,2,...,$H-1$ ：
  1. for $j$ = 0,1,2,...,$W-1$ ：
    1. ${\displaystyle \begin{alignat}{4} & A_{L+1}[k,&& j]=A_L[k,j]+&&\omega^{kW}A_L[k,j+W]+&& \omega^{2kW}A_L[k,j+2W]\\ & A_{L+1}[k+H,&& j]=A_L[k,j]+\Omega&&\omega^{kW}A_L[k,j+W]+\Omega^2&& \omega^{2kW}A_L[k,j+2W]\\ & A_{L+1}[k+2H,&& j]=A_L[k,j]+\Omega^2&&\omega^{kW}A_L[k,j+W]+\Omega&& \omega^{2kW}A_L[k,j+2W] \end{alignat} }$

ちなみに、ここで $\Omega$ と表した部分が 2 基底 FFT では $\exp(-2\pi i/2)=-1$ となるため 2 基底 FFT の一方は単純な引き算になっており、乗算を行う必要がないため演算量が大きく削減されている。

具体的な演算数は複素数乗算、複素数加算がそれぞれ $8n\log_3n$ 回ずつであるが、 $\Omega^2=\overline\Omega$ であることを利用することで、実数乗算が $\dfrac{20}{3}n\log_3 n \simeq 4.21n\log_2n$ 回、実数加算が $8n\log_3n \simeq 5.05n\log_2n$ 回となる。ほぼ同数のデータに対する 2 基底 FFT とくらべて 2 倍弱の演算量となることが分かる。

4 基底 FFT

4 の倍数になる $n$ については常に偶数となるため、2 基底 FFT があれば演算そのものは可能であるが、4 基底 FFT を導入することで演算量を削減することができる。

まずは 3 基底 FFT と同様に構成することで 4 基底 FFT の基本的なアルゴリズムが出来上がる。以下、$n=4^e$ とする。

for $L$ = 0,1,2,...,$e-1$ ：
1. $H=4^L$, $W=4^{e-L-1}$
2. for $k$ = 0,1,2,...,$H-1$ ：
  1. for $j$ = 0,1,2,...,$W-1$ ：
    1. ${\displaystyle \begin{alignat}{4} & A_{L+1}[k,&& j]=A_L[k,j]+&\omega^{kW}A_L[k,j+W]+& \omega^{2kW}A_L[k,j+2W]+&\omega^{3kW}A_L[k,j+3W]\\ & A_{L+1}[k+H,&& j]=A_L[k,j]-&i\omega^{kW}A_L[k,j+W]-& \omega^{2kW}A_L[k,j+2W]+&i\omega^{3kW}A_L[k,j+3W]\\ & A_{L+1}[k+2H,&& j]=A_L[k,j]-&\omega^{kW}A_L[k,j+W]+& \omega^{2kW}A_L[k,j+2W]-&\omega^{3kW}A_L[k,j+3W]\\ & A_{L+1}[k+3H,&& j]=A_L[k,j]+&i\omega^{kW}A_L[k,j+W]-& \omega^{2kW}A_L[k,j+2W]-&i\omega^{3kW}A_L[k,j+3W] \end{alignat} }$

ここで $4=2\times2$ であることを利用して計算量を減らすことを検討しよう。つまり中間ステップとして 2 基底 FFT のような形で演算をまとめることができる。

for $L$ = 0,1,2,...,$e-1$ ：
1. $H=4^L$, $W=4^{e-L-1}$
2. for $k$ = 0,1,2,...,$H-1$ ：
  1. for $j$ = 0,1,2,...,$W-1$ ：
    1. ${\displaystyle \begin{alignat}{4} & a_+=&& A_L[k,j&]+\omega^{2kW}A_L[k,j+2W]\\ & a_-=&& A_L[k,j&]-\omega^{2kW}A_L[k,j+2W]\\ & b_+=& \omega^{kW}&A_L[k,j+W&]+\omega^{3kW}A_L[k,j+3W]\\ & b_-=& \omega^{kW}&A_L[k,j+W&]-\omega^{3kW}A_L[k,j+3W] \end{alignat}}$
    2. ${\displaystyle \begin{alignat}{4} & A_{L+1}[k,&& j]=a_+ + b_+\\ & A_{L+1}[k+H,&& j]=a_- - ib_-\\ & A_{L+1}[k+2H,&& j]=a_+ - b_+\\ & A_{L+1}[k+3H,&& j]=a_- + ib_- \end{alignat} }$

ちなみに 4 基底 FFT では 3 基底 FFT でいう $\Omega$ に相当する数が $\exp(-2\pi i/4)=-i$ であるために、本来なら演算すべき（$i$ をかける）部分が計算対象（実部と虚部）を取り換えるだけですむのでより効率的になる。この点から言えば複素数型を扱える言語でも複素数値を 2 個の実数値として扱う事を勧めたい。

以上の点を踏まえて計算回数を求めてみると、 $3n\log_4n=\dfrac{3}{2}n\log_2n$ の実数乗算と $\dfrac{11}{2}n\log_4n=\dfrac{11}{4}n\log_2n$ の実数加算となるので、 2 基底 FFT と比較すると実数演算量が 15％削減されることになる。

$r$ 基底 FFT

4 基底 FFT の冒頭部分や 3 基底 FFT と同様にすることで任意の自然数 $r>1$ について $r$ 基底 FFT を構成することが可能である。より一般的に、データ数 $n$ が \[ n = \prod_{k=0}^{m-1} r_k = r_0 \cdot r_1 \cdot \cdots r_{m-1} \]

で表される時の FFT が構成できる。 $r_k$ は 2 以上の自然数であればどのような順序で並んでいても構わない。このとき $r_k$ の順序に基づいて以下のようなアルゴリズムが構成される。なお、第 $L$ 回目のループで $A_L$ は $H_L\times r_LW_L$ の行列であり、1 次元データとの対応は $A_L[k,j]=a_{r_LW_Lk+j}$ となる。

$H_0=1$
$W_0=n$
for $L=0,1,2,\cdots,m-1$ ：
1. $W_{L+1} = W_L \div r_L$
2. for $k=0,1,2,\cdots,H_L-1$ ：
  1. for $j=0,1,2,\cdots,W_L-1$ ：
    1. for $t=0,1,2,\cdots,r_L-1$ :
      1. $A_{L+1}[k+tH_L,j] = {\displaystyle \sum_{s=0}^{r_L-1}} \Omega^{st} \omega^{skW_{L+1}} A_L[k,j+sW_{L+1}]$
3. $H_{L+1} = r_LH_L$

ちなみに $k$と$j$、$t$と$s$ のループについては互いに依存関係が無いのでそれぞれ入れ替えても問題ない。また 3 基底 FFT でも述べたように $\Omega^{-st} = \overline{\Omega^{st}}$ が成り立つことを利用することで演算回数を減らすことができる。

また、いくつかの基底では基数に依存した最適化を行うことで演算数を削減することができる。例えば 4 基底 FFT では $\Omega=i$ との乗算を実質的に省くことができた。他にも 5 基底 FFT では $\cos(2\pi/5)=\dfrac{\sqrt{5}-1}{4}$、 $\cos(4\pi/5)=-\dfrac{\sqrt{5}+1}{4}$ から $\cos(4\pi/5)=-\dfrac12-\cos(2\pi/5)$ という形を利用でき、 8 基底 FFT では 4 基底 FFT と同じ手法に加えて $\cos(2\pi/8)=\sin(2\pi/8)=\dfrac{1}{\sqrt{2}}$ であることが利用できる。

演算回数

ここまでにいくつかの具体的な基底について、各基底の特徴を利用した演算効率化を紹介したが、ここではそのような効率化を行わない前提で一般的な FFT の演算量を求める。まずデータ数 $n$ が \[ n = \prod_{k=1}^{m} r_k^{e_k} \]

であるとき、1 つ 1 つの基底に対する演算量は表 1 のようになる。（具体的手段については $r$ 基底 FFT を参照。）

表1．`r` 基底 FFT の演算回数
	複素数演算回数	実数演算回数
乗算回数	$(r_k-1) ne_k$	$4(r_k-1) ne_k$
加算回数	$(r_k-1)ne_k$	$4(r_k-1)ne_k$

そのため全体としての演算回数は \[ \text{(実数乗算回数)} = \text{(実数加算回数)} = 4n \sum_{k=1}^{m} (p_k-1) e_k \]

となる。$\Omega^{st}$ の対称性を利用する場合は実数乗算が約半分になる。

特に最近のプロセッサは演算速度に対するメモリ読み書きの時間的コストが高いためキャッシュメモリに入りきらないサイズのデータが演算対象になる場合には「単位演算量当たりのデータ量」が重要になる。

$r$ 基底 FFT について考えるとデータ量が $O(r)$、演算回数が $O(r^2)$ であるため基本的には基底 $r$ が大きい方が有利である。しかし本質的にはレジスタの数やメモリ上の値を直接演算に用いる方式か、といった事柄が関わってくるので一概に大きい基底の方が良いとは限らない。