雑記
The tale of π
[FT02]から引用する分。基本的に日本語訳します。
πの精度
宇宙の大きさを原子の精度で知るためには，πは39桁あれば良い。
パリのπ
パリにある "Palais de la Decouverte" (発見館？) というギャラリーでは 1937 年に装飾として Shanks が計算した 707 桁のπの値を木製の数字で並べた。 これは 1945 年に Ferguson が計算記録を更新(とともに Shanks の528桁目以降が誤りであることを明らかに)するまで末尾の 180 桁は間違ったまま。
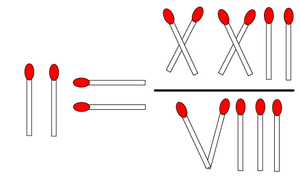
πの輪
ローマンアルファベット(A, B, C, …, Z)を環状に並べ，左右対称な文字 (A, H, I, …, Y)を消すと，残った文字のグループは JKL のグループから順に 3, 1, 4, 1, 6 文字のグループになっており，πの近似値 3.1416 になっている。
→
Telegraphic π
次の文は1991年1月2日に Daily Telegraph が報じたものである。誤りを見つけなさい。
The team includes David and Gregory Chudnovsky, who won a place in the Guinness Book of Records by computing pi, the ratio between the diameter and the radius of a circle, to more than a thousand million decimal places.
(訳文書くと見つけやすいミスなので英文のまま。)
ローマ数字でπ
次の状態からマッチ棒を1本動かして等式が正しくなるようにしなさい。（画像をクリックすると解答）
○○兄弟
Chudnovsky 兄弟は David Chudnovsky が兄，Gregory Chudnovsky が弟。
π素数
$[x]$ をガウス記号，つまり $x$ を超えない最大の整数を取る関数とするとき， $[10^n\pi] = \{ 3,\ 31,\ 314,\ \cdots\}$ のうち素数はどの程度あるのかという話。
既知のものは少ない。3($n=0$), 31($n=1$), 314159($n=5$), 31415926535897932384626433832795028841($n=37$) の他， $n=16207,\ 47576,\ 78072$ が知られている[FW04]。 私の調査範囲では $n\leq 103922$ で他は全て合成数である。
超次元球体
円の面積が $\pi r^2$，円周長が $2\pi r$，球の体積が $\frac{4}{3}\pi r^3$， 表面積が $4\pi r^2$ であることは知られている。 これ以上の $d$ 次元における(概念的な意味での)体積 $V_d(r)$ と表面積 $S_d(r)$ を以下のように定義する。
\[ V_d(r)=\int_{X_d}d\nu \quad \left({\rm where}\ X_d : \sum_{j=1}^d x_j^2 \leqq r^2 \right), \quad S_d(r) = \frac{d}{dr}V_d(r) \]これらは漸化的に以下のように計算でき，一般式として解ける。
\[ V_d(r)=\int_{-r}^r V_{d-1}(\sqrt{r^2-x^2})dx \] \[ V_d(r)=\frac{1}{(d/2)!}\pi^{d/2}r^d, \quad S_d(r)=\frac{d}{(d/2)!}\pi^{d/2}r^{d-1} \]これを展開したものと，$r=1$ を代入した数値は 表 1 に示したようになる。 $V(1)$ は 5 次元で，$S(1)$ は 7 次元で最大値を取る。
| 次元 | 体積 | 表面積 | ||
|---|---|---|---|---|
| $d$ | $V_d(r)$ | $V_d(1)$ | $S_d(r)$ | $S_d(1)$ |
| 1 | $2r$ | 2 | 2 | 2 |
| 2 | $\pi r^2$ | 3.14 | $2\pi r$ | 6.28 |
| 3 | $\dfrac43\pi r^3$ | 4.19 | $4\pi r^2$ | 12.57 |
| 4 | $\dfrac12\pi^2r^4$ | 4.93 | $2\pi^2r^3$ | 19.74 |
| 5 | $\dfrac8{15}\pi^2r^5$ | 5.26 | $\dfrac83\pi^2r^4$ | 26.32 |
| 6 | $\dfrac16\pi^3r^6$ | 5.17 | $\pi^3r^5$ | 31.01 |
| 7 | $\dfrac{16}{105}\pi^3r^7$ | 4.72 | $\dfrac{16}{15}\pi^3r^6$ | 33.07 |
| 8 | $\dfrac1{24}\pi^4r^8$ | 4.06 | $\dfrac13\pi^4r^7$ | 32.47 |
| 9 | $\dfrac{32}{945}\pi^4r^9$ | 3.30 | $\dfrac{32}{105}\pi^4r^8$ | 29.69 |
| 10 | $\dfrac1{120}\pi^5r^{10}$ | 2.55 | $\dfrac1{12}\pi^5r^9$ | 25.50 |