円周率.jp (http://xn--w6q13e505b.jp/define/arctan.html)

まずは高校までの課程で習う三角関数の復習をする．

$x$ 軸の正の部分に該当する半直線を、 原点を中心として反時計回りに $\theta$ だけ回転させたとき、 この半直線と単位円との交点を $(x, y)$ とする。

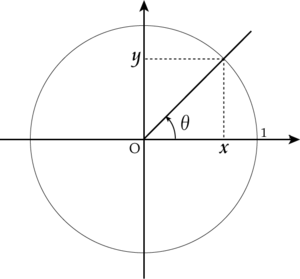
このとき三角関数 $\sin\theta$，$\cos\theta$，$\tan\theta$ を以下のように定義する。

\[ \sin\theta = y,\ \cos\theta = x,\ \tan\theta = \frac{y}{x} \]

また、高校までの課程では使うことは無いがそれぞれの逆数にも別名がついている。

\[ \sec x = \frac{1}{\cos x},\ \csc x ＝ \frac{1}{\sin x},\ \cot x = \frac{1}{\tan x} \]

逆正接関数 $\arctan$ （atan や $\tan^{-1}$ と書かれることもある） はこの $\tan$ の逆関数であり、

\[ \tan x = y \Leftrightarrow \arctan y = x \]

が成り立つ。 $\tan$ が周期 $\pi$ で周期関数となるのとは対称に $\arctan$ は周期 $\pi$ を持った多価関数であるが、 ここでは $-\frac{\pi}{2}\leq \arctan x \lt \frac{\pi}{2}$ を取るものとする。

同様に $\sin$ の逆関数は $\arcsin$ （asin，$\sin^{-1}$）， $\cos$ の逆関数は $\arccos$ （acos，$\cos^{-1}$）という。

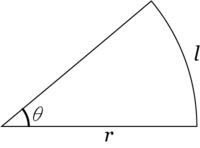
半径 $r$ の扇形における円弧の長さ $l$ について

\[ \theta = \frac{l}{r} \]

として角度 $\theta$ を定義する時、その単位をラジアン (rad) と呼ぶ。

よく知られている度数法との比較をすると $180^{\circ}$ が $\pi$ ラジアンと等しい。 1 周分の角度が $360^{\circ}$ で、円周長が $2\pi r$ なので $360^{\circ}$ が $2\pi$ に相当するというのが分かりやすいかもしれない。

多くのプログラム言語ではこの $\arctan$ に相当する計算ができる関数 atan(x) がある． ただしいずれの場合も多値関数としての返り値を出せないので 上記と同様に $-\pi/2\leq\arctan x\lt\pi/2$ の範囲を返すことが多い。 また本来特徴的な入力値である $\pm \infty$ がプログラムとしては扱いにくい他、 極座標とユークリッド座標との変換に用いやすい様に $(x, y)$ から偏角を出す atan2(y, x) 関数（値域は $-\pi\leq$ atan2(x,y) $\lt\pi$） も用意されている場合がある。