3<π<4 の証明
証明 1 (円周長を用いた証明)
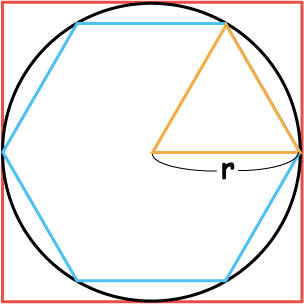
半径が r の円と, それに内接する正六角形,外接する正方形を図 1 に示した. ここで
\[ ({\rm 正六角形の周の長さ}) \lt ({\rm 円周の長さ}) \lt ({\rm 正方形の周の長さ}) \]が成り立つ.
正六角形の一辺の長さは $r$ であるため,正六角形の周の長さは $6r$ である. 同様に正方形の周の長さは $8r$ になる。 このことから
\[ 6r \lt 2\pi r \lt 8r \] \[ \therefore 3 \lt \pi \lt 4 \]が示された.
(正六角形の周の長さ) < (円周の長さ) について
2 点 A,B を結ぶ曲線が,$y=y(x)$ と表せる時,その長さ $l$ は
\[ l = \int_0^x \sqrt{1+\{y'(t)\}^2} dt \]と計算できる.
これを利用して,正六角形の一辺と, それに対応する円弧について考える. 正六角形の頂点が原点に,それに接続する一辺が $x$ 軸になるように座標を取る.
このとき,正六角形の辺を表す式は $y(x)=0$ となるため一辺の長さ $l=r$ である. 一方,円弧を表す式では $y'(x)^2 \gt 0$ となる $x$ が存在するため $l\gt r$ になる.
証明 2 (面積を用いた証明)
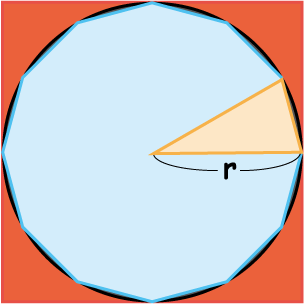
半径が $r$ の円と, それに内接する正十二角形,外接する正方形を図 2 に示した. ここで
\[ ({\rm 正十二角形の面積}) \lt ({\rm 円の面積}) \lt ({\rm 正方形の面積}) \]が成り立つ.
二等辺三角形の面積は $\dfrac14r^2$ となるため, 正十二角形の面積はその 12 倍,$3r^2$ であり, 正方形の面積は $4r^2$ である. ここで円の面積は $\pi r^2$ であることから
\[ 3r^2 \lt \pi r^2 \lt 4r^2 \] \[ \therefore 3 \lt \pi 4 \]が示された.