Newton 法
多倍長での計算で除算や平方根の計算を行う際に用いられる Newton 法、 ならびに Newton-Raphson 法を紹介する。 これらは本来は方程式 $f(x)=0$ の実数根を求める方法であるが、 適当な $f(x)$ を設定することで逆数や平方根といった値を求めることができるので 多倍長計算でよく用いられる。
Newton 法
まずは Newton 法について説明する。
なお、単に「ニュートン法」と言う場合に Newton-Raphson
法を指す場合もあるというより Newton-Raphson
法の方を指す方が多いので注意してほしい。
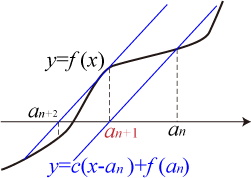
Newton 法では図 1 にあるように $y=f(x)$ 上の適当な点 $(a_0, f(a_0))$ からスタートし、 点 $(a_n, f(a_n))$ を通る傾き $c$ の直線と $x$ 軸の交点座標を$a_{n+1}$ とする、という処理を繰り返して解を求める。 図 1 から分かる通り、定数 $c$ の選び方によって 収束の速さや収束半径などが違ってくる。
数式を用いてアルゴリズムを記述すると \[ 0 = c(a_{n+1} - a_n) + f(a_n) \] \[ \therefore a_{n+1} = a_n - \frac{1}{c} f(a_n) \]
という漸化式になる。 この中で定数 $c$ や初期値 $a_0$ は任意に設定できるが、 多倍長計算を用いた逆数や平方根への適用を考える場合は 単精度で求められる値をそのまま使うと便利である。
Newton-Raphson 法
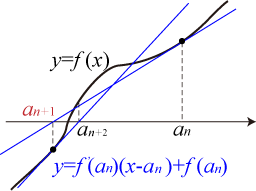
Newton-Raphson 法は Newton 法における定数 $c$ を $f(x)$ の導関数 $f'(a_n)$ で置き換えたもの、つまり図 1 の青線が常に曲線 $y=f(x)$ の接線になるようにしたもの(図 2)である。
別の見方をすれば、$f(x)$ を $x=a_n$ で 1 次まで Taylor 展開近似させて解を得る方法でもある。 とりあえず数式として表すと Newton 法と同様の式展開をして \[ a_{n+1} = a_n - \frac{f(a_n)}{f'(a_n)} \]
となる。
この方法は2次近似として知られる。 つまり $f(x)=0$ の根を $r$ とすると \[ |r-a_{n+1}| \leq C|r - a_n|^2 \]
となる。勿論 $C|r-a_n|<1$ でなければ収束の保証はない。
適用例
このNewton-Raphson 法を用いて 冒頭に挙げた除算と平方根の近似値を求める漸化式を求めてみよう。
除算
除算は、正確には逆数の近似と乗算を組み合わせる事によって求める。 なので Newton-Raphson 法を適用させて求める値そのものは逆数となる。
多倍長数 $A$,$B$ について $B\div A$ を求めようとするとき、 $x=1/A$ が根になっている $f(x)$ として \[ f(x) = \frac{1}{x} - A \]
を定義する。これにNewton-Raphson 法を適用させることで漸化式 \[ a_{n+1} = a_n(2 - Aa_n) = a_n + a_n(1 - Aa_n) \]
を得ることができる。 この漸化式を必要な回数繰り返すことで逆数 $1/A$ の近似値を求められるので \[ B \cdot a_n \]
で目的の商を求められる。
逆数を求める際に使った漸化式での誤差を計算すると \[ \frac{1}{A} - a_{n+1} = A\left(\frac{1}{A} - a_n\right)^2 \]
となり、2 次近似であることが確認できる。
平方根
平方根は $f(x)=x^2-A$ を設定することで直接 $\sqrt{A}$ を求めることもできるが、漸化式内で演算コストの高い多倍長除算が必要となる。 そのため、平方根の逆数を求め元の数との乗算により平方根を求めるという手法を取る。
数 $A$ (多倍長数でも単精度数でも構わない) について $\sqrt{A}$ を求めようとするとき、 \[ f(x) = \frac{1}{x^2} - A \] \[ \therefore a_{n+1} = \frac{1}{2} a_n (3 - Aa_n^2) = a_n + \frac{1}{2} a_n (1 - A a_n^2) \]
により $\dfrac{1}{\sqrt{A}}$ を得、 $\sqrt{A} = A \times \dfrac{1}{\sqrt{A}}$ として平方根を得る。
計算例
逆数の計算例として、$1/7=0.14285714\cdots$ を計算する。 結果を知っている分、どの程度正確なのかが分かりやすいだろう。
本来コンピュータで計算をする場合は初期値も有効数字 16 桁程度の値を使うがここでは 0.1 を初期値とする。 また漸化式も含めた全体のアルゴリズムをプログラム風に書くと
A := 7 # 逆数を求める値
x := 0.1 # 初期値設定
delta := 1 - x * A # 誤差計算
while (|delta| > eps) { # 精度チェック
x := x + x * delta
delta := 1 - x * A # 誤差計算
}
と、これだけのことである。この時の x
と delta の値は表 1 のようになる。
| ループ | x
| delta
|
|---|---|---|
| 0 回目 | 0.1
| 0.3
|
| 1 回目 | 0.13
| 0.09
|
| 2 回目 | 0.1417
| 0.0081
|
| 3 回目 | 0.14284077
| 0.00011461
|
| 4 回目 | 0.1428571409806497
| 0.0000000131354521
|
| 5 回目 | 0.14285714285714283249427116122937
| 0.00000000000000017254010187139441
|
また平方根の計算例として $1/\sqrt{2}=0.707106\cdots$ を計算してみよう。 初期値は有効数字 1 桁分の計算として 0.7 とすると
A := 2 # 平方根を求める値
x := 0.7 # 初期値設定
delta := 1 - x2 * A # 誤差計算
while (|delta| > eps) { # 精度チェック
x := x + x * delta / 2
delta := 1 - x2 * A # 誤差計算
}
となる。この時の各変数の値は表 2 のようになる。
| ループ | x
| delta
|
|---|---|---|
| 0 回目 | 0.7
| 0.02
|
| 1 回目 | 0.707
| 0.000302
|
| 2 回目 | 0.707106757
| 0.000000068409885902
|
| 3 回目 | 0.707106781186546283451619907
| 0.000000000000003509934446881563618293673456195202622702
|
ちなみにここの例で各値は計算している桁全てを表示しているが実際にはそれほど必要ない。 例えば 3 回目のループで得られた結果と そのうち正しい部分だけに切り詰めた数とのそれぞれの 2 乗を計算してみると \[ \begin{eqnarray} & & 0.707106781186546283451619907^2 &=& 0.499999999999998245032776559218190853163271902398688649\\ & & 0.70710678118654^2 &=& 0.4999999999999894 \end{eqnarray} \]
と、計算する桁数は倍以上違うのに 2 乗した結果の誤差には 1 桁しか違いがないので 上手く有効桁数を調整することで演算量を削減する事ができる。
計算量の削減
ここでは [JT04] に倣って逆数平方根 $1/\sqrt{A}$ の計算量を削減する方法を考えよう。
Newton-Raphson 法は 2 次収束なので $a_k$ が $n$ 桁正しいとすると、 $a_{k+1}$ は約 $2n$ 桁正しいということになる。 また $a_{k+1}$ と $a_k$ の上 $n$ 桁は一致しているので $\Delta a_k = |a_{k+1} - a_k|$ は約 $n$ 桁の有効桁数で十分ということが分かる。 このように考察していくとループ内での各計算ステップでの実質有効桁数は表 3 のようになるのでそれ以上の精度を計算しないようにすることで計算時間や メモリ量を節約することができる。
| 計算/変数 | 桁数 |
|---|---|
| $a_k^2$ | ($n$ 桁) $\times$ ($n$ 桁) $\Rightarrow$ ($2n$ 桁) |
| $Aa_k^2$ | ($2n$ 桁 or 1 桁) $\times$ ($2n$ 桁) $\Rightarrow$ ($2n$ 桁) |
| $1-Aa_k^2$ | $1 -$ ($2n$ 桁) $\Rightarrow$ ($n$ 桁) |
| $\Delta a_k = a_k(1-Aa_k^2)/2$ | ($n$ 桁) $\times$ ($n$ 桁) $\Rightarrow$ ($n$ 桁) |
| $a_k+\Delta a_k$ | ($n$ 桁) $+$ ($n$ 桁) $\Rightarrow$ ($2n$ 桁) |
補足しておくと $a_k$ が $n$ 桁正確に $1/\sqrt{A}$ を表しているので $Aa_k^2$ の約 $2n$ 桁のうち上約 $n$ 桁は $0.999\cdots$ もしくは $1.000\cdots$ のようになり、次の $1-Aa_k^2$ で約 $n$ 桁の精度になる。